blog kali ini saya coba mengumpulkan informasi tentang Ukuran Pemusatan Data dalam ilmu statistika.
semoga bermanfaat yah buat kalian yang cari informasi soal hal ini.. yuk lansung bahas dibawah ini.
Pengertiannya sendiri dari Ukuran Pemusatan Data menurut wikipedia adalah " sembarang ukuran yang menunjukkan pusat segugus data, yang telah diurutkan dari yang terkecil sampai yang terbesar atau sebaliknya dari yang terbesar sampai yang terkecil." yang kegunaannya untuk membandingkan dua (populasi) atau contoh. Nilai ukuran pemusatan ini dibuat sedemikian sehingga cukup mewakili seluruh nilai pada data yang bersangkutan.
Untuk perhitungan ukuran pemusatan data yang digunakan ada 3 yaitu dengan cara :
- penghitungan rata-rata (Mean),
- perhitungan nilai tengah (Median),
- perhitungan nilai yang sering muncul (Modus).
Mean (Rata-rata)
Mean atau rata-rata hitung adalah nilai yang diperoleh dari jumlah sekelompok data dibagi dengan banyaknya data. metode ini yang paling banyak digunakan untuk menggambarkan ukuran tendensi sentral (skor tunggal). Definisi Mean dapat dapat dinyatakan dengan persamaan untuk data Sampel dan data Populasi.
Mean data Sampel dinyatakan dengan:
Sementara Mean untuk data Populasi dinyatakan dengan:
keterangan :
∑ = lambang penjumlahan semua gugus data pengamatan
n = banyaknya sampel data
N = banyaknya data populasi
 = (dibaca "x-bar") = nilai rata-rata sampel
= (dibaca "x-bar") = nilai rata-rata sampelμ (huruf kecil Yunani dibaca “mu”) = nilai rata-rata populasi
a. Rata-rata hitung (Mean) untuk data tunggal
Contoh :
Diketahui nilai siswa hasil ujian Statistik seperti berikut: 20; 40; 50; 60; 60; 70; 70; 70; 80; 90. Hitunglah nilai rata-rata dari nilai ujian statistik tersebut.
Penyelesaian:
n = 10 (banyaknya data)
b. Rata-rata hitung untuk Data Dikelompokkan.
Nilai rata-rata dari data yang sudah dikelompokkan bisa dihitung dengan menggunakan formula berikut:
dimana:
fi = frekuensi data ke-i
n = banyaknya sampel data
= nilai rata-rata sampel xi = data ke-i
Contoh :
Median (Nilai Tengah)
Median adalah nilai tengah dari kelompok data yang telah diurutkan (urutannya bisa membesar atau mengecil). Jika jumlah data ganjil, median = nilai paling tengah. Jika jumlah data genap, median = rata-rata dari dua nilai tengah, dengan kata lain, median terletak pada nilai ke: (n/2), "n" adalah banyaknya data pengamatan.
a. Median data tunggal :
Untuk menentukan median dari data tunggal, terlebih dulu kita harus mengetahui letak/posisi median tersebut. Posisi median dapat ditentukan dengan menggunakan formula berikut:
Median = (n+1)/2 dimana n = banyaknya data pengamatan.
- Jika banyaknya data n ganjil
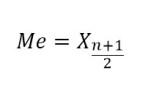
- Jika banyaknya data n genap
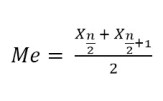
Keterangan:
Me = Median
n = jumlah data
x = nilai data
contoh ganjil :
Tentukan median : 6, 7, 6, 6, 5, 8, 7
setelah diurutkan data menjadi : 5, 6, 6, 6, 7, 7, 8 (ganjil) yang mana n = 7 jika dihitung menggunakan rumus maka :
Me = x n + 1 = x (7+1) = x 4 dengan kata lain : nilai dari / urutan ke 4 = 6 ,
2 2
sehingga median untuk data tersebut adalah 6
Contoh genap :
tentukan median : 7, 7, 10, 8, 6, 6, 7, 8
setelah diurutkan data menjadi : 6, 6, 7, 7, 7, 8, 8, 10 (genap) yang mana n = 8 maka :
Me = x (8/2) + x (8/2)+1 = x 4 + x 5
2 2
dengan kata lain : nilai urutan ke 4 ditambah urutan ke 5 kemudian dibagi 2 = 7 + 7 = 7
2
b. Median data Kelompok
Untuk data berkelompok yang dinyatakan dalam bentuk tabel distribusi frekuensi:
Med = Lo + c ( ((n/2) – F)) / f )
dimana Med = median
Lo = batas bawah kelas median
c = lebar kelas
n = banyaknya data
F = jumlah frekuensi semua kelas sebelum kelas yang mengandung median
f = frekuensi kelas median
Contoh :
Tentukan nilai median dari tabel distribusi berikut :
Jawab :
Letak kelas median:
Setengah dari seluruh data = 40, terletak pada kelas ke-5 (nilai ujian 71-80)
Lo = 70,5,
c = 10
n = 80,
f = 24
f = 24 (frekuensi kelas median)
F = 2 + 3 + 5 + 13 = 23
diperoleh Tabel berikut:
Modus adalah data yang paling sering muncul atau memiliki frekuensi tertinggi. Modus dilambangkan dengan Mo. Beberapa kemungkinan tentang modus suatu gugus data:
- Apabila pada sekumpulan data terdapat dua modus, maka gugus data tersebut dikatakan bimodal.
- Apabila pada sekumpulan data terdapat lebih dari dua modus, maka gugus data tersebut dikatakan multimodal.
- Apabila pada sekumpulan data tidak terdapat modus, maka gugus data tersebut dikatakan tidak mempunyai modus
Modus dari data tunggal adalah data yang paling sering muncul.
Contoh :
Tentukan modus dari data berikut !
4, 8, 7, 4, 6, 3, 6, 8, 6, 3
Jawab :
bila kita urutkan terlebih dahulu maka menjadi : 3, 3, 4, 4, 6, 6, 6, 7, 8, 8
Data yang paling sering muncul adalah 6, maka Mo = 6
b. Modus dalam Distribusi Frekuensi
Modus untuk data terdistribusi frekuensi adalah:
Mo=Lo + c (f1/ (f1+f2))
dimana:
Mo = modal = kelas yang memuat modus
Lo = batas bawah kelas modal
c = panjang kelas modal
fmo = frekuensi dari kelas yang memuat modus (yang nilainya tertinggi)
f1= fmo – fmo-1 = frekuensi kelas modal – frekuensi kelas sebelumnya
f2 = fmo – fmo+1 = frekuensi kelas modal – frekuensi kelas sesudahnya
Contoh :
Diketahui data terdistribusi frekuensi seperti Tabel belikut:
Tentukan nilai median dari tabel distribusi frekuensi pada Tabel di atas.
Penyelesaian:
Kelas modus =kelas ke-5
Lo = 71-0.5 = 70.5
f1 = 24 -13 = 11
f2 = 24 – 21 = 3
c = 10
okeh sampai disini dulu informasinya semoga bermanfaat untuk kalian dan menambah pengetahuan kalian mengenai statistika. kita ketemu lagi di pembahasan berikutnya. terima kasih sobat net.. ^^
http://winnerstatistik.blogspot.com/2009/05/penggunaan-mean-median-dan-modus-2.html
https://myreisa.wordpress.com/2017/09/26/statistika-ukuran-pemusatan-data-mean-median-modus/
https://www.risetdata.com/blog/2015/03/23/manakah-ukuran-pemusatan-nilai-tengah-yang-lebih-baik-mean-atau-median/
https://www.berpendidikan.com/2016/09/pengertian-dan-rumus-cara-menghitung-nilai-rata-rata-mean-beserta-contoh-soal-mean-data-tunggal-dan-data-berkelompok.html
modul 5 online 4 uniersitas esaunggul
wikipedia.com






