STATISTIKA - PROBABILITAS MARGINAL, PERMUTASI, KOMBINASI

PROBABILITAS MARGINAL

Suatu kejadian yang terjadi bersamaan dengan kejadian lainnya dimana kejadian lainnya tersebut dipengaruhi kejadian pertama. Probabilitas marginal juga dapat dikatakan probabilitas tak bersyarat.

mari kita terapkan pada suatu contoh agar dapat dimengerti :

contoh;

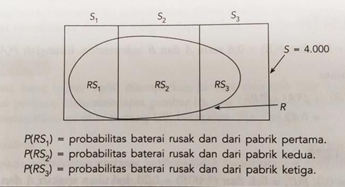
misalkan kita memproduksi suatu jenis baterai di tiga pabrik yang peralatan dan karyawannya berbeda. Produksi mingguan pabrik pertama (S1 = 500), pabrik kedua (S2 = 2000), dan pabrik ketiga (S3 = 1500).Selanjutnya, misalkan diketahui besarnya nilai probabilitas barang rusak dari pabrik pertama, P(R/S1) adalah 0.020, probabilitas barang rusak dari pabrik kedua, P(R/S2) adalah 0.015, dan dari pabrik ketiga P(R/S3) adalah 0.030. baterai yang diproduksi pabrik tersebut digunakan untuk menyuplai pabrik mobil. Dengan demikian, pabrik mobil setiap minggunya menerima suplai baterai sebanyak 4000, dari S1+ S2 + S3 (ingat, S adalah ruang sampel). Jika satu baterai dipilih secara acak,maka:

Apabila pemilik pabrik tersebut mengambil 1 batrai secara acak, berapa probabilitasnya bahwa baterai yang diambil tersebut rusak.

P(R) = probabilitas barang rusak, disebut probabilitasmarjinal.

Karena P(RS1) = P(S1)P(R/S1) kita peroleh rumus berikut: 

Probabilitas Marjinal = P(R) =∑𝑃(S1)P(R/S1)

Dengan rumus tersebut, kita dapat menghitung probabilitas bahwa baterai yang dipilih secara acak rusak, yaitu:

TEOREMA BAYES

Thomas Bayes (1702-1761) mengembangkan teori untuk menghitung probabilitas tentang sebab-akibat (cause) dari suatu kejadian berdasarkan pengaruh yang dapat diperoleh sebagai hasil observasi. yang bertujuan untuk memecahkan masalah pembuatan keputusan yang mengandung ketidakpastian (decision making under uncertainly).

contoh;

Suatu daftar pertanyaan dikirimkan kepada para responden untuk mengetahui penggunaan mobil keluarga. Kita anggap suatu nilai “a priori probability” bahwa daftar pertanyaan tersebut akan diisi oleh keluarga yang tinggal dijakarta adalah 0.5, probabilitas bahwa daftar pertanyaan diisi oleh mereka yang berpenghasilan tinggi adalah 0.3, berdasarkan pengalaman, probabilitas bahwa daftar pertanyaan yang dikirim kepada penduduk luar Jakarta diisi oleh mereka yang berpenghasilan tinggi sama dengan 0.2, kita gunakan symbolberikut:

Misalkan daftar pertanyaan yang sudah diisi sudah kita terima, sedangkan kode mengenai tempat tinggal responden sudah dihapus. Dengan demikian, kita tidak mengetahui apah responden tersebut tingal di luar Jakarta atau di Jakarta. Kalau daftar pertanyaan tersebut diisi oleh keluaarga tersebut bertempat tinggal di luar Jakarta, P(A1/A)?

Penyelesaian:

PERMUTASI

Permutasi adalah penyusunan kembali suatu kumpulan objek dalam urutan yang teratur dan berbeda dari urutan semula. "urutannya diperhatikan"

• permutasian merupakan bentuk khusus aplikasi kaidah perkalian.
• misalkan jumlah objek adalah n maka.

1. urutan pertama dipilih dari n objek,
2. urutan kedua dipilih dari n-1 objek,
3. urutan ketiga dipilih dari n-2 objek,
4. ...., dan seterusnya.
5. urutan terakhir dipilih dari 1 objek yang tersisa.

Banyaknya permutasi = n(n-1)(n-2) ...(1) 

FAKTORIAL

Hasil kali bilangan bulat positif dari 1 sampai n disebut n faktorial, ditulis n!

n! = 1.2.3.....(n-2)(n-1).n 

catatan :

• 1! = 1
• 0! = 1

PERMUTASI

Permutasi dari seluruh obyek rumusnya adalah :

nPn = n!

Contoh;

untuk tiga huruf A, B, dan C.
a. hitunglah banyaknya permutasi dari tiga huruf A, B dan C
b. daftarlah permutasi dari tiga huruf A, B dan C

jawab :

a. disini n = 3, sehingga  banyaknya permutasian dari 3 huruf A, B dan C adalah;
    3P3 = 3! = 3.2.1 = 6
b. permutasian dari tiga huruf A, B dan C adalah  ABC, ACB, BAC, BCA, CAB, CBA,



Permutasian sebanyak x dari n obyek :

Contoh :

Apabila ada 3 orang mahasiswa (ABC) dipermutasikan masing-masing 2, maka permutasi sebagai berikut :

Contoh :

Misalnya suatu dafter memuat 10 rencana investasi yang dikemukakan oleh direksi perusahaan kepada suatu dewan komisaris, dimana setiap anggota dewan komisaris diminta untuk memberikan penilaian terhadap 5 rencana investasi tersebut yang dianggal feasible. Ada berapa cara ranking dari 10 rencana investasi tersebut kalau diambil 5 setiap kali?

Jawab :

Dari soal diketahui n = 10, dan x = 5, maka:

Permutasi siklis / keliling

Permutasi dari obyek yang membentuk suatu lingkaran, dirumuskan sebagai :

(n-1)!

Contoh :

Sekelompok mahasiswa terdiri dari 10 orang akan mengadakan rapat dan duduk mengelilingi sebuah meja ada berapa carakah kesepuluh mahasiswa tersebut dapat diatur pada sekeliling meja tersebut?

Jawab :

n = 10
P10 = (10-1)! = 9.8.7.6.5.4.3.2.1 = 362880 cara

Contoh :

4 orang duduk mengelilingi meja bundar, maka susunan melingkar 4 orang tersebut adalah?

Jawab : 

P = (n-1)! = (4-1)! = 3! = 3.2.1 = 6

Permutasian sebanyak x dari n obyek dengan pengembalian, dirumuskan dengan :

Contoh :

3 orang mahasiswa (ABC) dipermutasikan sebanyak 2, dengan pengembalian, maka jumlah permutasinya :

KOMBINASI

Kombinasi merupakan cara pemilihan obyek tanpa menghiraukan urutan obyek tersebut. kombinasi dipilih sebanyak x dari obyek sebanyak n, 

Contoh :

Dalam sebuah sekolah telah diseleksi 5 orang siswa yang berbakat dan mahir batminton. Berapa banyaknya cara pemilihan yang mungkin jika dipilih 3 orang siswa untuk mewakili sekolah dalam turnamen barminton ?

Jawab :